人口增长与总患癌人数之间的关系建模

作者：GARFIELDTOM
邮箱：coolerxde@gt.ac.cn

摘要

本文基于2006~2019年日本大阪市历史人口数据以及总癌症患病数统计数据，大致可以划分为三个阶段。通过对2006~2010年第一个正增长阶段的分析和建模，得出了基础的人口增长以及癌症患病人数之间的患病率的关系。之后基于2011-2012年两点数据拟合癌症发病模型在后期（2013-2018年）低估的问题，提出了一种优化方法。首先，通过考虑到人口老龄化可能会导致患癌人数的上升，引入人口老龄化参数。后发现直接线性乘以人口老龄化参数仍然不能够很好的表征，在后期患癌人数的显著增加。再考虑到图形特征引入在指数上的多项式拟合方法。在引入二次多项式不含常数项的修正方案后发现，尽管两点数据限制了参数独立估计，加入非线性修正有效捕捉了发病率加速增长的趋势，为最小数据建模提供了改进方向。

关键词： 人口下降，癌症发病率，指数建模，比例分析，非线性优化

问题重述

问题背景

癌症作为现代医学中最为棘手的疾病之一，自被发现以来，就成为了生命科学、公共卫生、社会环境以及生育健康等各个学科所关注的重点问题。作为一种因原癌基因或抑癌基因突变，细胞节律异常的疾病，对其进行数学建模以及预测在人口当中的发病情况尤为重要。在没有较好的治疗方案下，人口的自然增长必然会伴随着癌症确诊人数的提升。当人口增长平缓而癌症发病人数升高时，可侧面反映人口结构的变化，以及社会卫生情况等的变化。对于相关领域具有重要的意义。

问题重述

本次建模以2006~2019年日本大阪市历史人口数据以及总癌症患病数统计数据位基础[1]，构建科学的数学模型。系统性的分析癌症疾病与人口之间的关系，包括：

• 探究人口与癌症患病人数之间的相关性；
• 构建人口增长以及癌症患病人数增长模型；
• 研究两个模型之间的关联性以及换算方法；
• 研究在发生已知的重大变化时，两模型是否会发生分歧。

通过上面的4个步骤的研究，以期提出一个在一段时间内合理的对人口以及癌症的换算方法，以及当换算失效时是否可以作为一种预警的可行性探索。

问题分析

癌症作为一种人人都有不为零的概率，不在外界干扰下自发地患病的疾病，理论上可以与人口总数相绑定，并呈现出某种关系。故而尝试使用阻滞型人口模型预测人口，并且尝试验证该模型是否可以同样用于预测癌症患病人口。并且研究它们之间的关系。

基本假设

• 在研究期间，没有发生比较严重的环境污染事件，每一个人自然患癌的几率在研究期间没有较大的变动；
• 在研究期间，没有发生人口年龄结构的结构变化，人口年龄基本呈现正三角形分布或者老龄化倾向或者正在老龄化，并且没有较大变动；
• 在研究期间，没有发生人口上线等的较大变动，并且对于癌症的治疗多倾向于保守治疗方案，暂无可以直接完全治愈的普遍治疗方法。

符号说明

符号	说明	单位
$t$	年份	年
$x(t)$	t 年时期的总人口	千人
$y(t)$	t 年时期的总患癌人口	千人
$r$	人口自然增长率	1

模型建立与求解

5.1 人口与患癌总人口之间的相关性

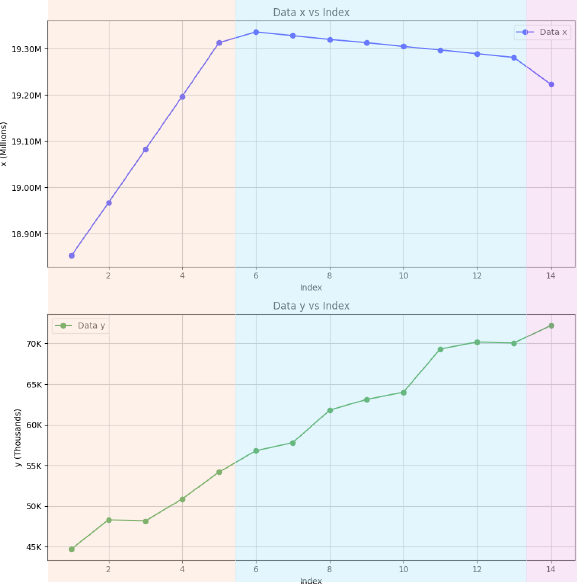
Figure 1 Plot between Total Population and Total Number of Cancer Patients

如Figure 1，通过绘制人口总数的折线图和患癌总人数的折线图，并且进行对比可以发现，大体上，日本大阪市的人口增长和患癌变化的阶段可以划分为为：

• 正增长阶段（正相关）：2006~2010年；
• 老龄化阶段（负相关）：2011~2018年；
• 突变阶段点（负相关）：2019年。

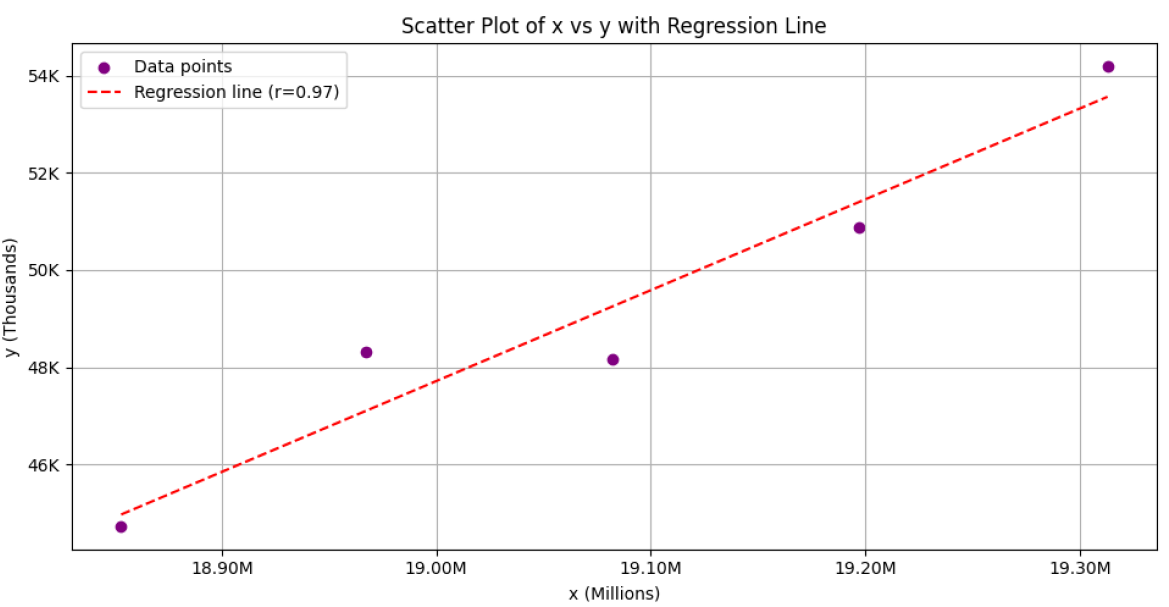
Figure 2 2006~2010, Showing a Positive Correlation Stage

从Figure 1中不难发现，在人口增长阶段（2006年~2010年），总人口数与总患癌人数呈现出明显正相关，并且使用Pearson相关系数（使用公式i计算）来衡量两组数据之间的线性相关性。得到 $R=0.97$ ，如Figure 2，说明具备极强的线性相关。则可以通过某种关系，在人口增长时期，使用人口总数换算得总癌症患病数。

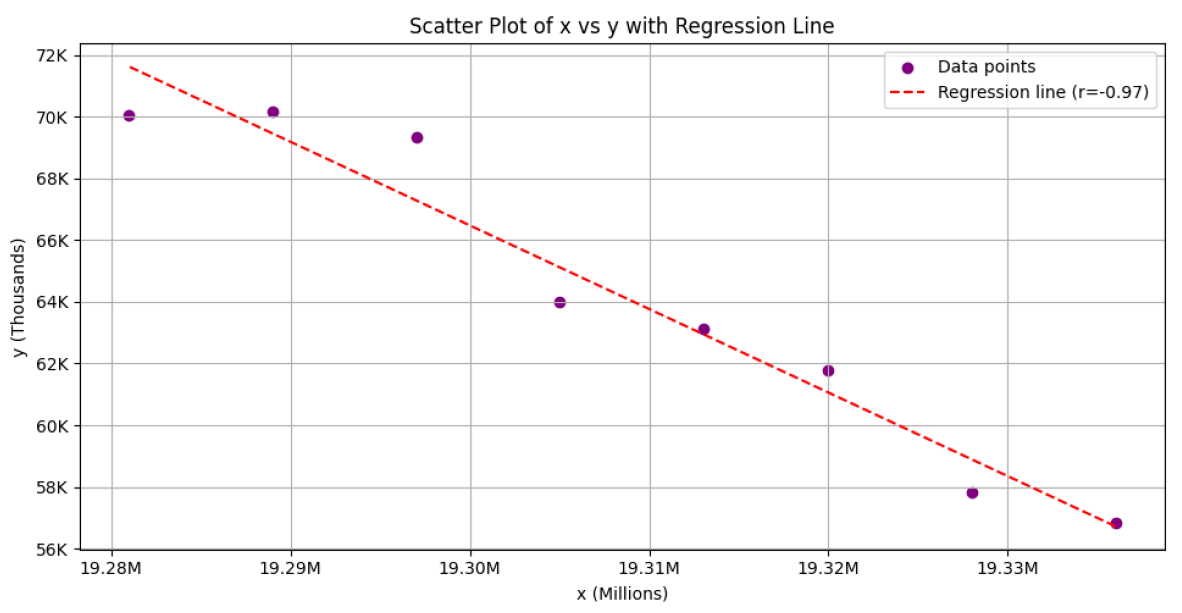
Figure 3 2011~2018, Showing a Negative Correlation Phase

如Figure 3，当出现人口老龄化以及人口负增长时，不妨结合生物学常识，此时的总癌症患病数不会随着人口的减少而减少，反而会因为老年人的增加而增加，若再验证它们之间的相关性，得到 $R=-0.97$ ，显现出强烈的负相关性。

5.2 构建人口增长模型及老龄化模型

5.2.1 以正增长阶段（正相关）为数据集，构建模型

设时刻 $t$ 时人口为 $x(t)$ ，单位时间内人口增长率为 $r$ ，则 $\Delta t$ 时间内增长人口为：
$$ x(t+\Delta t) - x(t) = x(t) \cdot r \cdot \Delta t $$
当 $\Delta t \to 0$ ，得到微分方程：
$$ \frac{dx}{dt} = rx \quad \text{且} \quad P(0)=x_0 $$
则： $x(t) = x_0 \cdot e^{rt}$ ，且待求参数为 $x_0$ ， $r$ 。通过公式ii中的处理方法进行建模。

正增长阶段最终人口模型为：
$$ x(t) = 18,853,000 \cdot e^{0.0073t} $$
增长率 $r=0.0073$ 表示人口每年增长约 $0.73\%$ ，验证模型：

• $t=1$: $x(1) = 18,853,000 \cdot e^{0.0073} \approx 18,999,991$ ，实际为 18,967,000 ，偏差约 32,991 （ $0.17\%$ ）。
• $t=4$: $x(4) = 18,853,000 \cdot e^{0.0292} \approx 19,309,560$ ，实际为 19,313,000 ，偏差约 3,440 （ $0.02\%$ ）。
  模型拟合合理，但人口增长近似线性（也即每年增加约11.5万人），指数模型可能略有偏差。

正增长阶段最终癌症患者模型为：
$$ y(t) = 44,729 \cdot e^{0.0424t} $$
增长率 $k \approx 0.0424$ 表示癌症患者数每年增长约 $4.24\%$ 。验证模型：

• $t=1$: $y(1) = 44,729 \cdot e^{0.0424} \approx 46,674$ ，实际为 48,314 ，偏差约 1,640 （ $3.4\%$ ）。
• $t=4$: $y(4) = 44,729 \cdot e^{0.1696} \approx 53,077$ ，实际为 54,187 ，偏差约 1,110 （ $2.0\%$ ）。
  模型拟合合理，尽管2007至2008年数据略有下降（48,314至48,171），可能是数据波动所致。

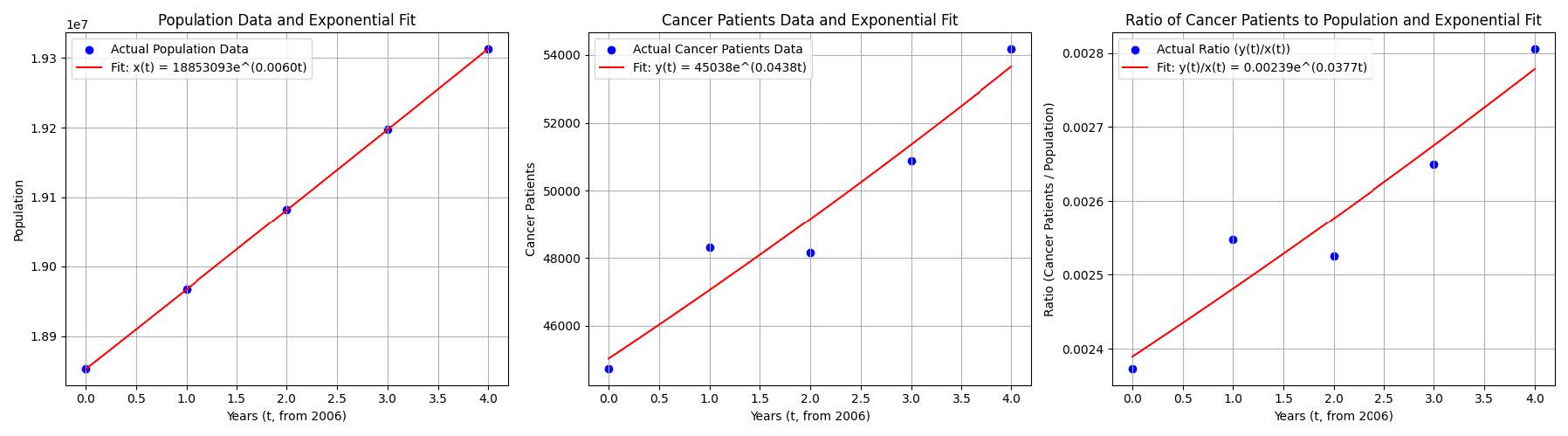
Figure 4 Fitted Curves of Population Growth, Number of Cancer Patients, and the Relationship between Them

此时，癌症患者与人口之间的比例关系可以表示为：
$$ \eta(t) = \frac{y(t)}{x(t)} = \frac{44,729 \cdot e^{0.0424t}}{18,853,000 \cdot e^{0.0073t}} \approx 0.00237 \cdot e^{0.0351t} $$
这表明，癌症患者占人口的比例随时间指数增长，增长率为 $0.0351$ （每年约 $3.51\%$）。例如：

• $t=0$ 时， $\eta \approx 0.00237$ （即 $0.237\%$ ）；
• $t=4$ 时， $\eta \approx 0.00273$ （即 $0.273\%$ ）。
  从0到4的微小变化，可能是导致Figure 2中微小的偏差的原因，并且说明了，患癌患者增长率 $k$ 和人口自然增长率 $r$ 确实存在关系。有趣的是，人口增长近似线性，而癌症患者增长显示更明显的指数趋势，这可能反映医疗诊断改善或人口年龄结构变化的影响。也就是说，现实情况下，部分的假设可能并不成立，导致了偏差。

5.2.2 以老龄化阶段（负相关）为验证集，验证所搭建的模型

我们已经得到了由人口增长拟合曲线与患癌患者增长曲线之间的关系式，如下：
$$ \eta(t) = \frac{y(t)}{x(t)} = \frac{y_0}{x_0} e^{(k-r)t} $$
则，此时，当我们得到人口增长拟合曲线之后，只需要通过两个癌症患者人数的数据（若为 $t=0$ 和 $t=1$ ），就可以求得 $\frac{y_0}{x_0}$ 以及 $k-r$。

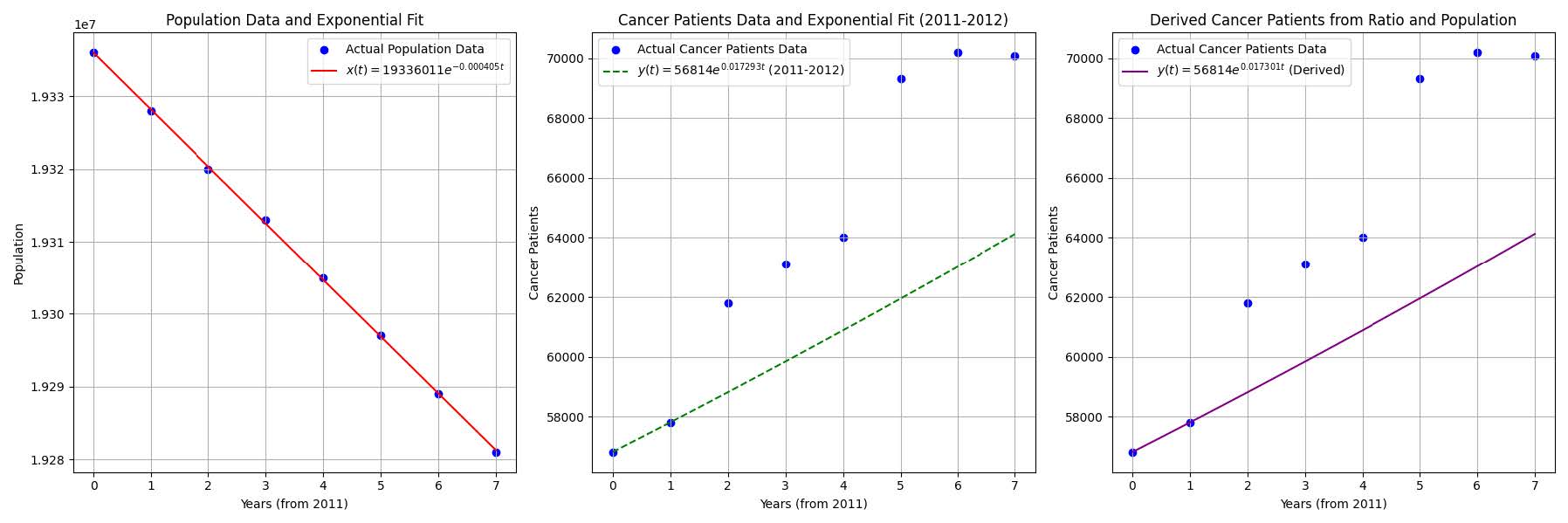
Figure 5 The Fitted Plots Were Calculated Using the Python Program

代入老龄化阶段（负相关）的人口数据，可以得到（ 该模型的误差范围为-0.00%至0.23%，精确度较高） ：
$$ x'(t) = 19,336,011 e^{-0.000405t} $$
仅用2011年和2012年的患癌患者人数数据（$t=0, 1$），可以计算得到 $\eta'$ 如下：
$$ \frac{y'_1(t)}{x'(t)} = 0.002938 e^{0.017751t} $$
也就是说患癌的可能性的年均增长约 $1.78\%$。并且可以得到癌症患者增长模型（两点数据）：
$$ y'_1(t) = 56,814 e^{0.017383t} $$
如Figure 5，发现这可能是因为癌症发病率在后期加速增长，受到老龄化或医疗因素的影响[2]。两点数据的局限性在于其仅捕捉短期趋势，长期预测需更多数据点。但是即使是使用全部数据，其拟合效果仍然较差。不过，比例模型 $\frac{y'_1(t)}{x'(t)}$ 的引入提供了从发病率角度理解趋势的视角，但其预测力同样受限于早期数据。2011-2012年的增长率（约 $1.74\%$ ）低于整体趋势（约 $2.97\%$-$3.03\%$ ），可能是因为癌症发病率在后期加速增长，未被早期数据捕捉。出现这种情况，或许是因为人口自然增长模型中，即使处于老龄化阶段，自然死亡和出生仍然还是相对稳定的。但是由于老龄化加剧，导致癌症的自然发病率会随着老龄化的进行而发生增大。

5.2.3 模型优化

鉴于当前仅使用2011年、2012年的两点数据的约束，并且结合老龄化对癌症发病率的潜在影响，在先前的指数增长模型 $y(t) = y_0 \cdot e^{kt}$ 基础上，引入老龄化调节项。
定义 $A(t)$ 为老龄化指数，用来衡量人口中老年人口（通常指65岁及以上）的比例。它被假设为一个随时间 $t$ 增长的函数，考虑到老龄化是自然发生的并且平均寿命在一个国家的短期内不会有显著改变。当人口出现负增长时，也就意味着这个国家进入了深度老龄化阶段，此时老龄化程度约 $25\%$ ，并且逐年增长，也就是：
$$ A(t) = \frac{x_{old}(t)}{x(t)} = \frac{x_{old}(0) \cdot e^{r_{old}t}}{x(0) \cdot e^{rt}} = \frac{x_{old}(0)}{x(0)} \cdot e^{(r_{old}-r)t} $$
其中，下角标old表示老年人， $r_{old}$ 也就是人口中老年人自然增长率。
因为 $r_{old}-r$ 通常较小，我们可以用线性近似（泰勒展开）简化指数函数：
$$ e^{(r_{old}-r)t} \approx 1+(r_{old}-r)t $$
从而，定义老龄化率 $a = \frac{x_{old}(0)}{x(0)}$ ：
$$ A(t) \approx a(1+(r_{old}-r)t) = a + a(r_{old}-r)t $$
已知， $r = -0.000405$ ；人口统计学认为开始人口自然负增长时，人口老龄化的初始值大约为倒三角形中最大的部分，也就是 $a \approx 0.25$ 。
为了估计 $r_{old}$ ，我们需要知道：在老龄化社会中，老年人口的增长率 $r_{old}$ 通常接近于零或略负（因高龄死亡），但由于中龄人口（45-64岁）逐渐进入老年阶段， $r_{old}$ 可能略高于总人口增长率 $r$ ，假设：
定义 $g = a(r_{old}-r)$ ，则 $r_{old}$ 在-0.0001至0.01之间（即老年人口减少较慢或略有增长且 $g$ 与 $r$ 之间的正差距一般不超过1个数量级）。
（1）若 $r_{old}=0$ （老年人口总量保持稳定），则：
$ g = a(0-r) = 0.25 \cdot (0 - (-0.000405)) = 0.25 \cdot 0.000405 = 0.00010125 $
这远低于0.005，说明老年人口不能完全稳定，必须有正增长。
（2）若 $g=0.005$ （半个数量级差异于 $r$ ）：
$ a(r_{old}-r) = 0.005 \implies 0.25 (r_{old} - (-0.000405)) = 0.005 $
$ r_{old} + 0.000405 = \frac{0.005}{0.25} = 0.02 $
$ r_{old} = 0.02 - 0.000405 = 0.019595 $
即老年人口年均增长率为 $1.9595\%$ ，远高于总人口的 $-0.0405\%$。
若 $r_{old}=0.019595$ ，老年人口从2011年（$t=0$）的 $0.25 \cdot 19,336,000 = 4,834,000$ 增长到2018年（$t=7$）老年人人口： $x_{old}(7) = 4,834,000 \cdot e^{0.019595 \cdot 7} \approx 5,526,000$ ；总人口 $x(7) \approx 19,336,011 \cdot e^{-0.000405 \cdot 7} \approx 19,281,000$ ；老龄化率： $A(7) = \frac{5,526,000}{19,281,000} \approx 0.2866$ 与 线性近似 $A(7) = a + gt = 0.25 + 0.005 \cdot 7 = 0.285$ 非常接近。说明我们第一次半数量级假设就已经很合理了。不过 $r_{old}=0.019595$ 可能是偏高的，因医疗进步和中龄人口老化速度较快。若实际情况中老年人口增长较慢（如 $0.5\%$-$1\%$ ），则 $g$ 会低于0.005。
不过，总归得到了：
$$ A(t) = 0.25 + 0.005t $$

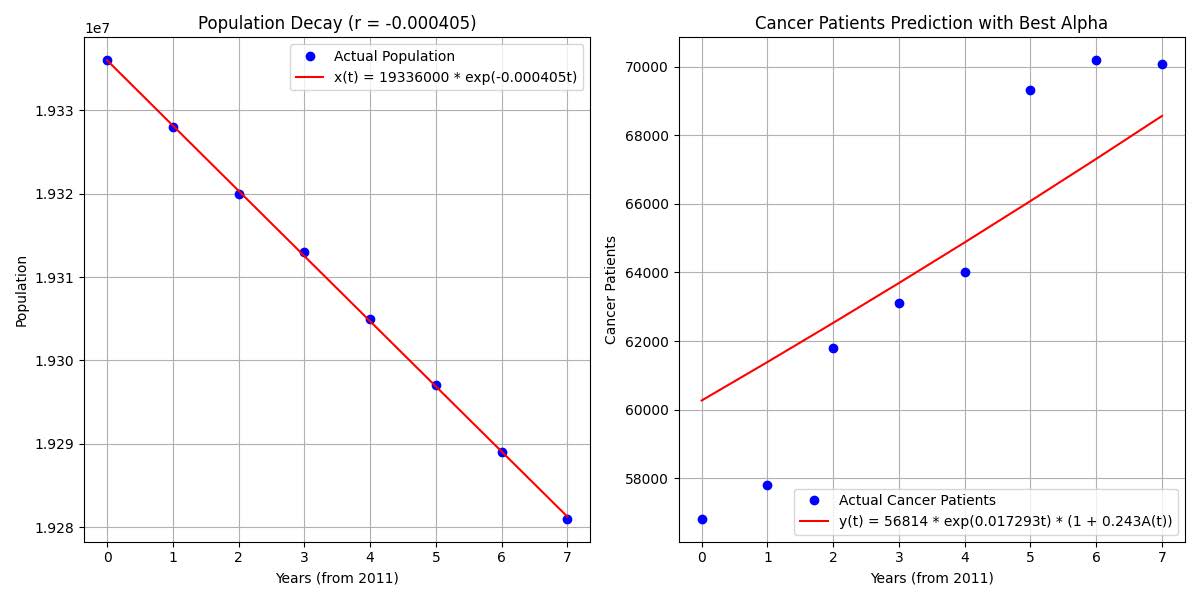
Figure 6 Predictions from a Linear Correction Model (Where the Impact Factor Is Calculated Automatically, Making R the Best Fit)

则修正模型为：
$$ y(t) = y_0 \cdot e^{kt} \cdot (1 + \alpha A(t)) $$
其中： $y_0$ 是初始患癌人数、 $k$ 为癌症自然增长率、 $A(t)$ 为老龄化指数、 $\alpha$ 为老龄化对癌症发病率的影响系数。
根据新的模型进行数学计算后，如Figure 6，发现，其在中间年份时，拟合效果较好，但在开始年份时，高估了患病率；在终结年份时，低估患病率。通过观察散点图，以及拟合操作可以猜测，指数项可能是二次函数多项式。不妨重新定义新的拟合函数如下：
$$ y(t) = y_0 \cdot e^{c_1 t^2 + c_2 t} \cdot (1 + \alpha A(t)) $$
其中，参数 $c_1$ 、 $c_2$ 和 $\alpha$ 由数据拟合得到。

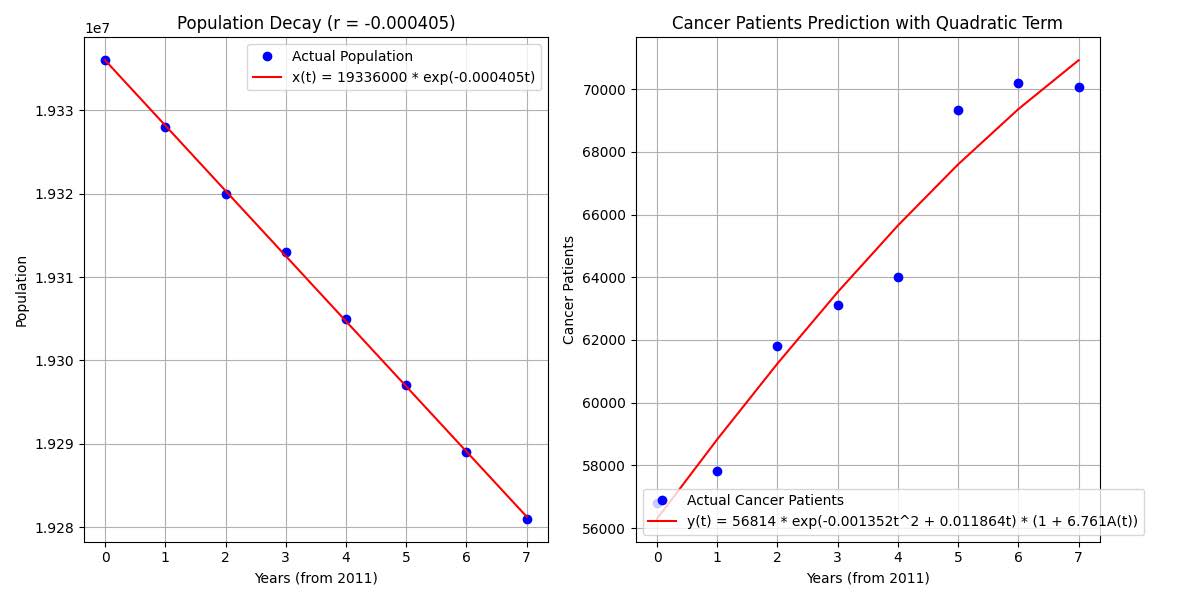
Figure 7 After Fitting the Function Image Using a Polynomial, It Can Be Noticed That the Result Becomes Very Good

使用计算机程序带入新的多项式拟合模型之后，可以发现，新的模型的拟合效果较好，可以在拥有极少参数量的情况下得到较好的模型效果。结合之前进行引入的发病率的考虑，该模型本质上考虑到了发病率，在人口老龄化阶段，因老年人口增加而呈现的非全自然增长情况。也就是说，随着年龄的增加，患癌概率也会随之增加，且在老龄化阶段，该增长趋势会更加明显。并且在第三阶段（2019年），患癌人数大致符合多项式修正后模型，但人口自然增长的下跌情况出现了明显转折。也可以说明其发病率在人群当中的变化并非是完全自然增长。

二次项修正后的癌症患者预测与实际值对比：

t	实际值	预测值	误差
0	56814	56295	-0.91%
1	57805	58831	+1.77%
2	61796	61248	-0.89%
3	63118	63528	+0.65%
4	64011	65651	+2.56%
5	69325	67602	-2.49%
6	70189	69363	-1.18%
7	70067	70921	+1.22%

六、结论

通过引入发病率的方式，我们可以加入一个二次项的方式来扩大后期的发病影响，以更好的使模型在人口老龄化的情况下有更好的拟合效果和预测效果。可以在较小数据量的情况下，得到患癌人口的数量。并且最终得到在人口老龄化阶段的拟合方程及具体参数如下(基于附录代码P5拟合结果)：
$$ y(t) = 56814 \cdot e^{-0.001352 t^2 + 0.011864 t} \cdot (1 + 6.6761 A(t)) $$
其中 $A(t) = 0.25 + 0.005t$。

在得到该方程的过程当中发现，当人口由正增长转向负增长时，患癌概率发生明显变化。由原先的自然患癌概率增长变更为含多项式的增长。并且在，2019年发生人口突变时，明显发现患癌人数的变化也发生突变。这也侧面说明了人口变化及年龄结构对患病率的潜在影响，也就是说，即使在每一个人都有一定概率患癌的情况下，当年龄结构发生显著变化时，也就表征在人口增长模型发生显著变化时，总体总人口患癌概率也将发生显著变化。

附录

附录1：公式

i. Pearson相关系数公式

$$ R = \frac{n(\sum xy) - (\sum x)(\sum y)}{\sqrt{[n\sum x^2 - (\sum x)^2][n\sum y^2 - (\sum y)^2]}} $$

ii. 指数增长模型的拟合

我们使用指数增长模型
$$ x(t) = x_0 \cdot e^{rt} $$
其中， $t$ 为2006年起的年数（ $t=0$ 对应2006年， $t=1$ 对应2007年，依此类推）。模型参数通过对自然对数 $\ln x(t)$ 进行的线性回归确定。
$$ \ln x(t) = \ln x_0 + r \cdot t $$
其中， $\ln x_0$ 为截距， $r$ 为斜率，通过线性回归计算参数，即：
$$ r = \frac{n \cdot (\sum t \cdot \ln x(t)) - (\sum t) \cdot (\sum \ln x(t))}{n \cdot (\sum t^2) - (\sum t)^2} $$
$$ \ln x_0 = \frac{\sum \ln x(t)}{n} - r \frac{\sum t}{n} $$

附录3：参考文献

1. 大阪国際がんセンター がん対策センター. (平成18年～令和元年). 「統計でみる大阪府のがん」. 大阪, 日本. [オンライン]. 利用可能: https://stat.osaka-gan-joho.net/
2. Jeong W, Choi DW, Kim W, Han KT. What is the relationship between the local population change and cancer incidence in patients with dyslipidemia: Evidence of the impact of local extinction in Korea[J]. Cancer Med, 2024, 13(7): e7169. doi: 10.1002/cam4.7169.