材料的凝固与气相沉积

知识点 9：平衡凝固

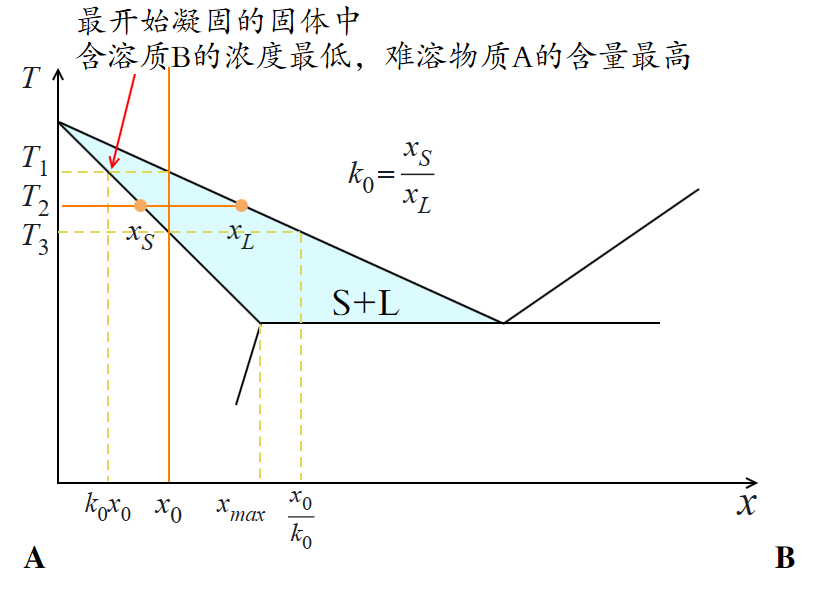
不妨定义分配系数，用于表征在总体含物质 B 量为 $C_0$ 时，物质 B 在凝固过程中于固体和液体中的分配比例情况如下：

在 A、B 二元组分相图中，显然凝固过程中固体和液体对物质 B 的分配是不同的。$C_0$ 代表物质 B 的含量百分数。当含 B 量为 $C_0$ 的溶液开始凝固时，首先凝固出的晶核含 B 量为 $k C_0$，此时含 B 量最小。随着晶核长大，固体中含 B 量不断上升，逐渐接近 $C_0$，最终完全凝固为含 B 量为 $C_0$ 的固溶体。

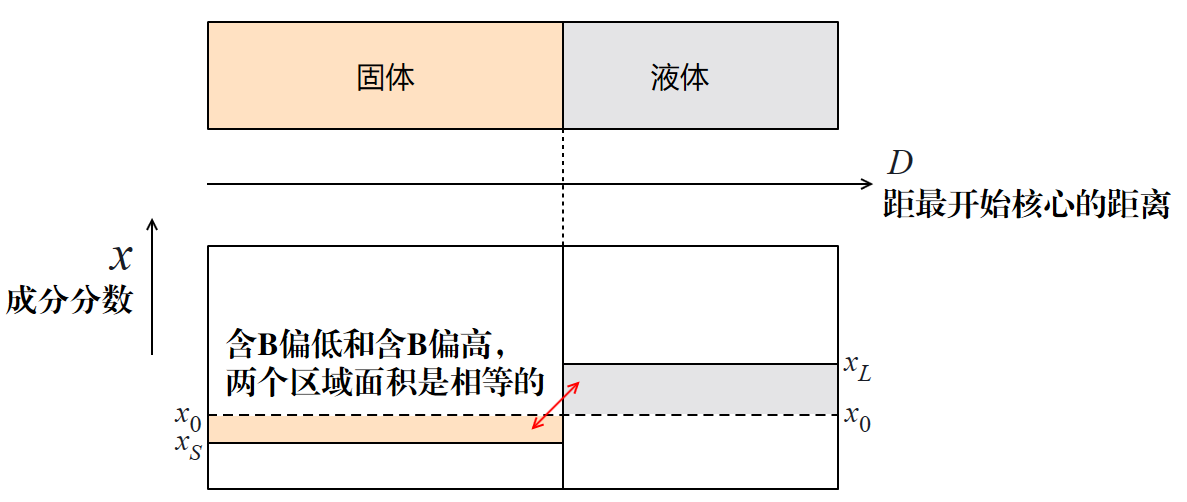
为保持整体物质 B 含量为 $C_0$，液体和固体中含 B 量会动态变化，且缺少物质 B 的面积与富余物质 B 的面积始终相等。假设固体和液体都能快速调整自身成分，则有：

$$ C_S = k C_L $$

其中，$C_S$ 和 $C_L$ 分别是固相和液相中物质 B 的浓度，$k$ 是分配系数。凝固进度可用 $f_S$ 表示（$f_S = 1$ 时完全凝固）。

知识点 10：不平衡凝固

固相内无扩散，液相内完全均匀化

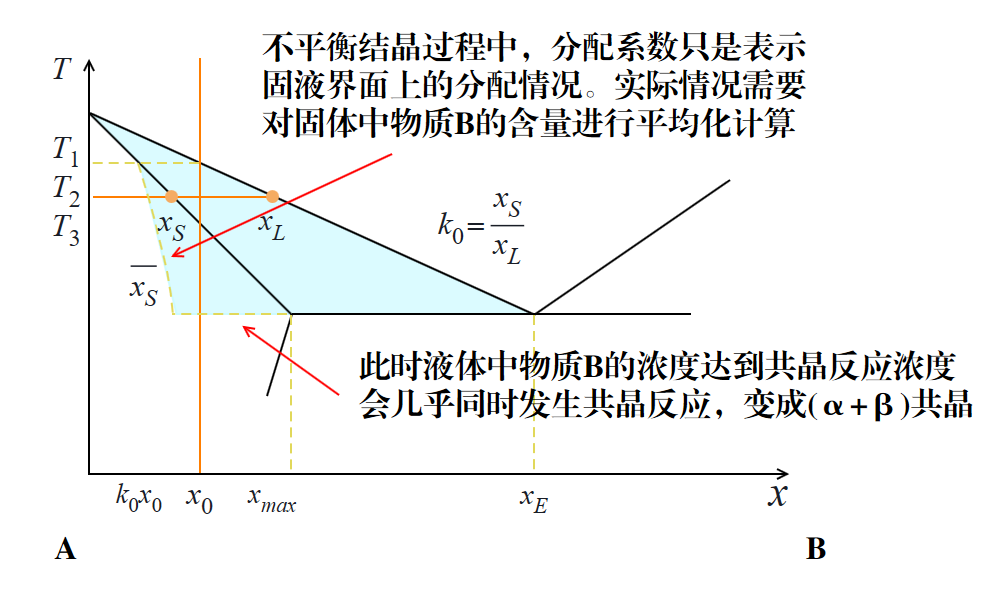
在实际凝固过程中，固体中的物质 B 无法快速均匀化，导致先凝固的部分含易溶物质 B 的浓度较低。分配系数 $k$ 仅在液固界面处有效，这使得平均固体溶质浓度偏离平衡位置。即使温度达到平衡凝固点，也不会完全凝固。只有当液体中物质 B 浓度达到共晶反应浓度 $C_E$ 时，剩余液体会在共晶反应温度 $T_E$ 下发生共晶反应，形成共晶。

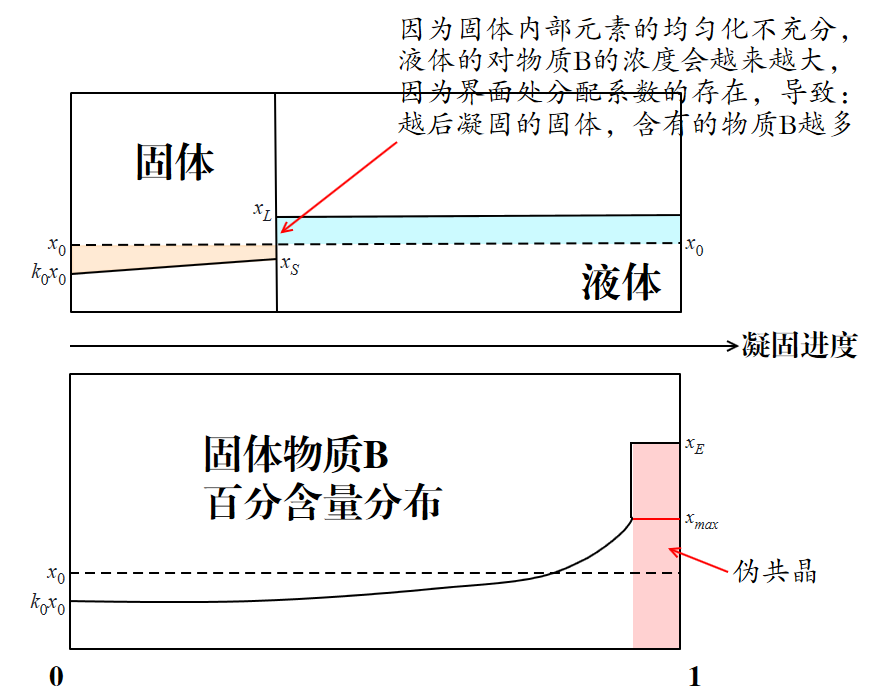
为更精确地描述这一过程，假设固液界面的横截面积为 $A$，可建立以下关系：

$$ C_L = \frac{C_0}{(1 - f_S)^{1 - k}} $$

代入初始条件：

• 当 $f_S = 0$ 时，$C_L = C_0$，满足初始条件；
• 当 $f_S \to 1$ 时，$C_L \to \infty$，符合接近完全凝固时浓度突然跃升的现象。此时，液体浓度达到 $C_E$，发生共晶反应，凝固结束。

固相内无扩散，液相内仅有扩散无对流

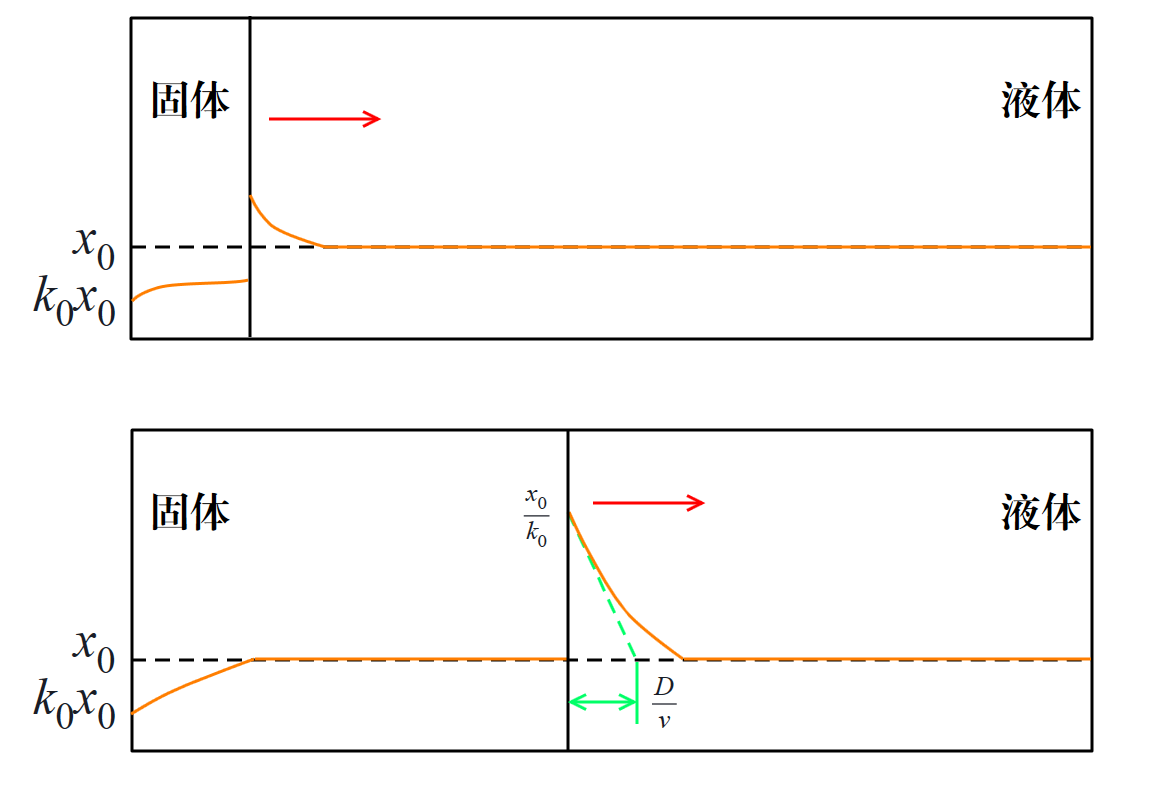
在一些粘稠液体中，仅存在扩散，热对流作用几乎可忽略，溶质原子无法完全均质化。初期，由于液体无法将富余溶质原子完全扩散，固液界面处的物质 B 浓度不断增大：

$$ C_L = C_0 (1 - f_S)^{-k} $$

当溶液中物质 B 浓度达到 $C_{L, \text{steady}}$ 时，在分配系数 $k$ 的作用下，凝固出的固体浓度稳定为 $C_S = k C_{L, \text{steady}}$，此时物质 B 的扩散与累积达到平衡。

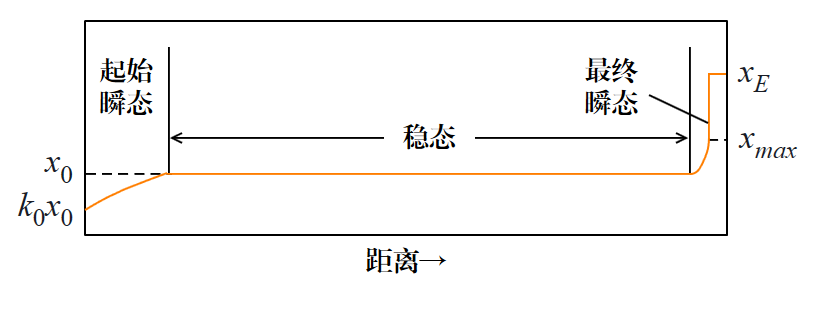
接近完全凝固时，由于液体体积有限，物质 B 浓度再次攀升，直到达到共晶反应浓度 $C_E$，发生共晶反应，完成凝固。这一过程如下所述：

• 初期：液相浓度随凝固进度逐渐增大；
• 中期：达到稳态，固体浓度稳定；
• 末期：液体浓度急剧上升至 $C_E$，共晶反应结束凝固。

作者：GARFIELDTOM
邮箱：coolerxde@gt.ac.cn