理论基础
液相传质的三种不同方式
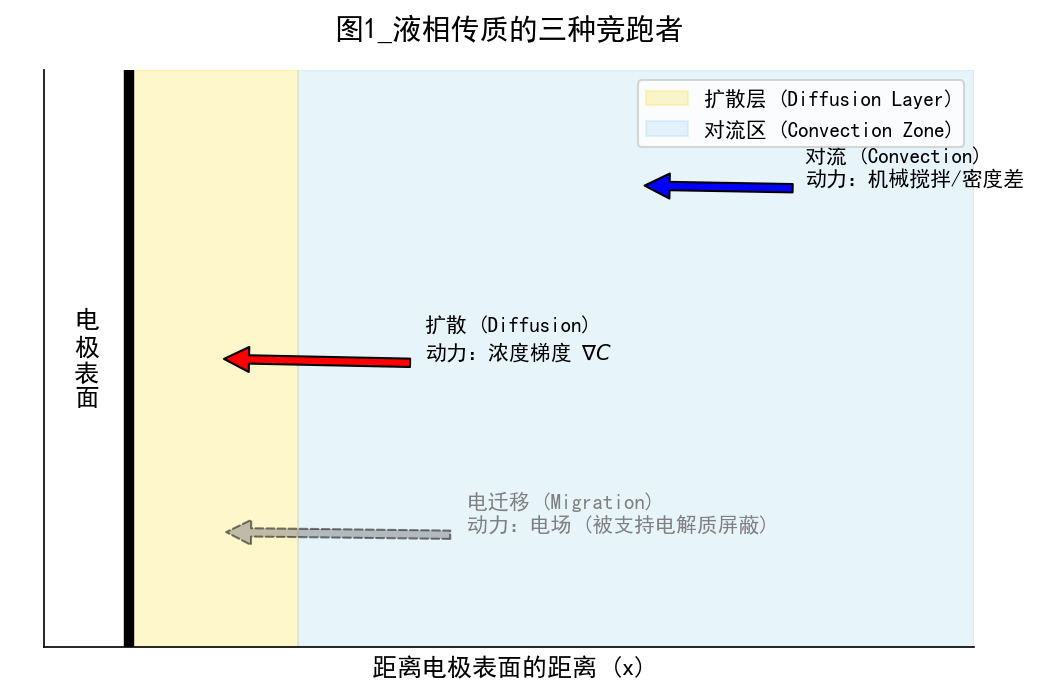
传质机制示意
在电解液中,离子的运动并非只有一种方式。我们可以将其想象为三种不同动力驱动的“竞跑者”。要研究纯粹的电化学反应,我们必须学会控制它们。
$$ J_{total} = J_{migration} + J_{diffusion} + J_{convection} $$
电迁移
由电场(电位梯度)驱动。这是电解池中通过电流的必要条件,但在研究电极表面反应动力学时,它是一个干扰项。因为它让计算变得极为复杂(电场与浓度场耦合)。
控制方法:加入大量“局外电解质”(支持电解质)。它们承担了绝大部分的离子导电任务,屏蔽了电场对反应离子的作用力,从而“剔除”电迁移项。
对流
由机械力(搅拌、旋转)或密度差(自然对流)驱动。它将物质从溶液本体“快递”到电极附近,但无法送达“最后一公里”(电极表面极薄的液层)。
控制方法:在稳态技术中(如旋转圆盘电极RDE),利用精确控制的对流来维持一个稳定的供给层;在暂态技术中(如静止循环伏安),则需严格避免对流,以免破坏扩散层。
扩散
由化学位梯度(浓度差)驱动。这是物质抵达电极表面的最后一步,也是必经之路。
核心逻辑:电极反应消耗了表面的粒子 $\rightarrow$ 表面浓度降低 $\rightarrow$ 与本体溶液形成浓度差 $\rightarrow$ 驱动本体粒子向表面移动。
菲克第一定律与稳态扩散模型
当我们通过搅拌或旋转电极建立起一个稳定的流体环境时,浓度分布不再随时间变化,这就是“稳态”。
流量与梯度的线性关系
菲克第一定律是所有扩散理论的基石。它告诉我们,流得有多快,取决于浓度坡度有多陡。
$$ J = -D \frac{dC}{dx} $$
能斯特扩散层假说
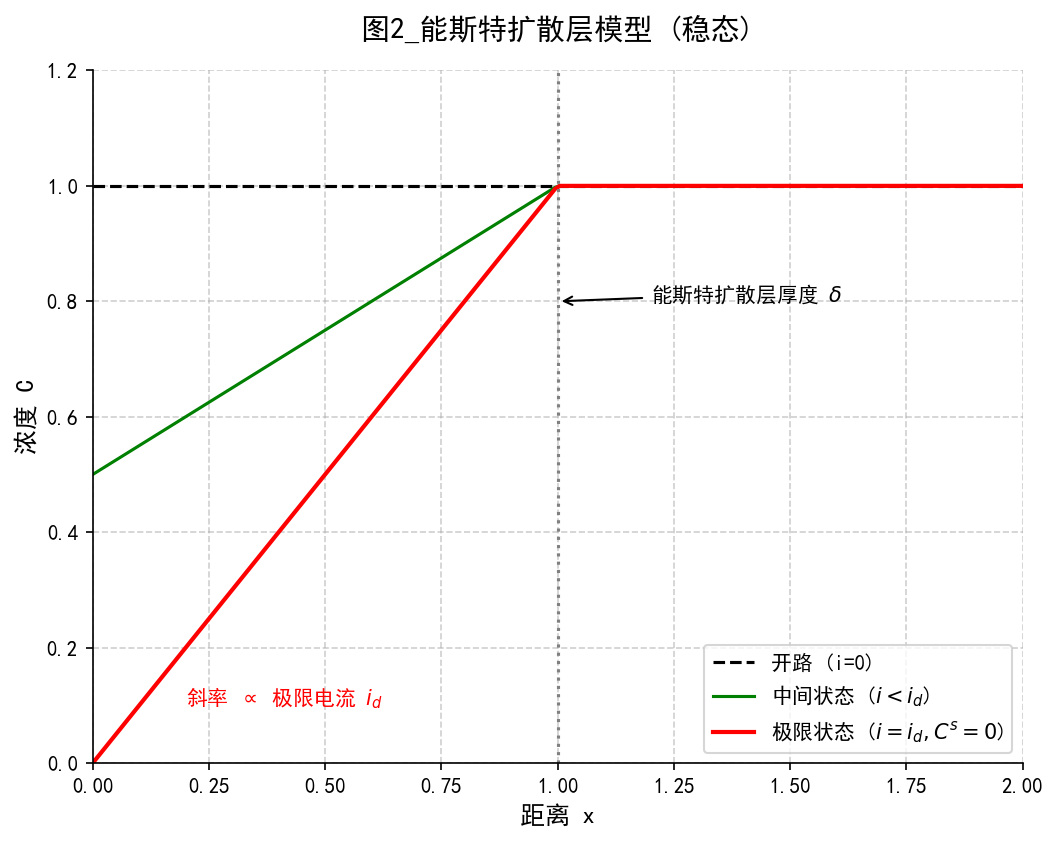
在真实流体中,流速靠近表面逐渐减为0。能斯特(Nernst)提出了一个简化的物理模型:假设在电极表面存在一层静止不动的液层,厚度为 $\delta$。在此层内只发生扩散,层外浓度维持为本体浓度 $C^0$。
能斯特扩散层模型
极限扩散电流的物理推导
电流 $i$ 直接正比于流量 $J$。
当电位极负,反应极快,电极表面的反应物来一个“吃”一个,导致表面浓度 $C^s$ 降为 $0$。此时浓度梯度达到最大值,电流也达到极限。
$$ \text{Gradient}_{max} = \frac{C^0 - 0}{\delta} $$
$$ i_d = nFA J_{max} = n F A D \frac{C^0}{\delta} $$
图像与概念的联系
这个公式揭示了为什么搅拌越快(对流越强),电流越大。
物理图像:搅拌压缩了停滞层厚度 $\delta$。
数学关系:$\delta$ 变小 $\rightarrow$ 分母变小 $\rightarrow$ 梯度变陡 $\rightarrow$ $i_d$ 变大。
这就是旋转圆盘电极(RDE)的Levich方程的物理本质:$\delta$ 被精确控制为与转速 $\omega$ 相关。
浓差极化的热力学解释
为什么电流还没到极限扩散电流时,电位就已经偏离了平衡电位?这是传质速度与表面浓度之间的博弈。
表面浓度与电位的纽带
电极电位并不直接控制电流,它控制的是电极表面的浓度比。只要是可逆反应,表面必须时刻遵守能斯特方程。
$$ E = E^{0'} + \frac{RT}{nF} \ln \frac{C_O^s}{C_R^s} $$
电流与表面浓度的定量关系
对于产物不溶(如金属沉积)的体系,我们假设 $C_R=1$。
任何时刻的电流 $i$ 对应着某个表面浓度 $C_O^s$:
$$ i = n F A D \frac{C^0 - C_O^s}{\delta} $$
极限电流 $i_d$ 对应着表面浓度为0:
$$ i_d = n F A D \frac{C^0}{\delta} $$
联立上述两式,消去常数项,我们得到了表面浓度与电流比值的无量纲关系:
$$ \frac{C_O^s}{C^0} = 1 - \frac{i}{i_d} $$
浓差极化公式的诞生
将上述表面浓度的表达式代回能斯特方程,就得到了教材中那个经典的极化曲线公式。它描述了$E$与$i$呈现出的S形曲线关系。
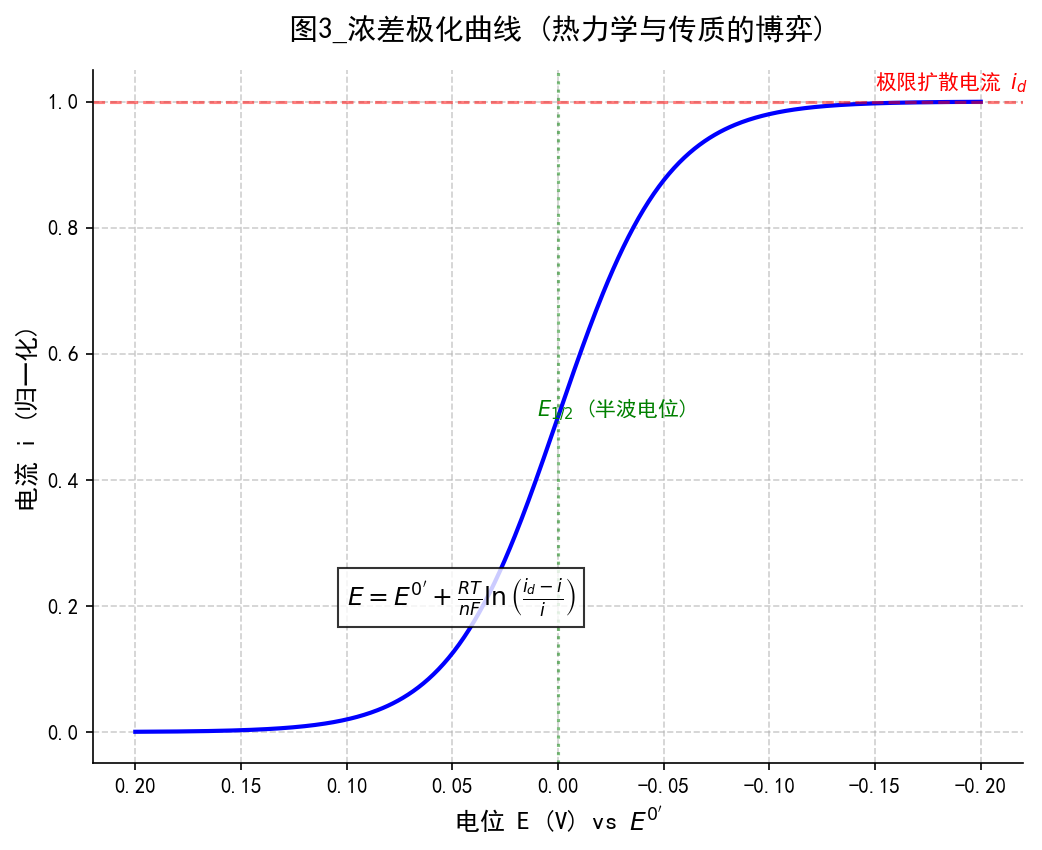
$$ E = E^{0'} + \frac{RT}{nF} \ln C^0 + \frac{RT}{nF} \ln \left( 1 - \frac{i}{i_d} \right) $$
图像理解
浓差极化曲线
当 $i$ 接近 $i_d$ 时,括号内趋近于0,对数项趋向负无穷,电位 $E$ 急剧负移。这就是极化曲线中出现“平台”的原因——即便电位再负,受扩散限制,电流也上不去了。
菲克第二定律与暂态扩散(时间的介入)
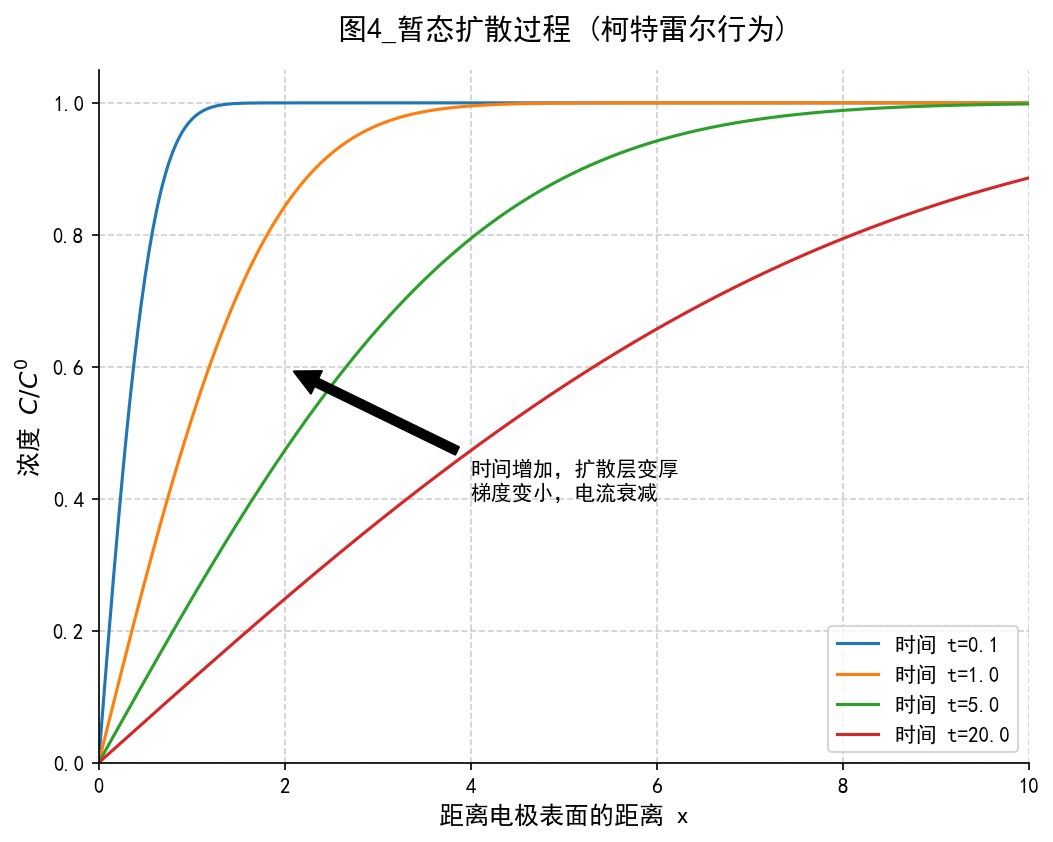
当我们停止搅拌,并在静止溶液中施加一个电信号时,扩散层不再是一个固定的厚度,它会随着时间向溶液深处“生长”。
非稳态的核心
浓度不仅随位置 $x$ 变化,还随时间 $t$ 变化。某一点浓度的变化率,等于流入与流出该点的流量差。
$$ \frac{\partial C(x,t)}{\partial t} = D \frac{\partial^2 C(x,t)}{\partial x^2} $$
柯特雷尔(Cottrell)行为的物理推导
对于恒电位阶跃(瞬间把电位拉得很负,使 $C^s=0$),我们需要求解上述偏微分方程。
利用拉普拉斯变换或误差函数求解,我们不必关注中间繁琐的数学过程,但必须记住最核心的物理结果——浓度分布图(PPT第23页)。
在 $x=0$ 处求导,我们得到了电流随时间衰减的规律:
$$ i(t) = \frac{n F A D^{1/2} C^0}{\sqrt{\pi} t^{1/2}} $$
非稳态扩散层的“有效厚度”
对比稳态公式 $i = nFADC/\delta$ 和暂态公式,我们可以定义出一个随时间变化的扩散层厚度 $\delta(t)$:
$$ \delta(t) = \sqrt{\pi D t} $$
图像与概念的深度绑定
这是一个非常美的物理结论。它告诉我们:
- 时间越短,扩散层越薄。所以在刚通电的微秒级瞬间,扩散层极薄,浓度梯度极大,电流无穷大。
- 随着时间推移,扩散波向外扩散。受影响的区域($\delta$)越来越厚,将反应物搬运过来的路程变长,浓度梯度变缓,因此电流按 $1/\sqrt{t}$ 衰减。
- 这就是为什么在微电极或快速扫描伏安法中能获得大电流密度的原因——我们在扩散层还没来得及变厚之前就完成了测量。
非稳态扩散分布
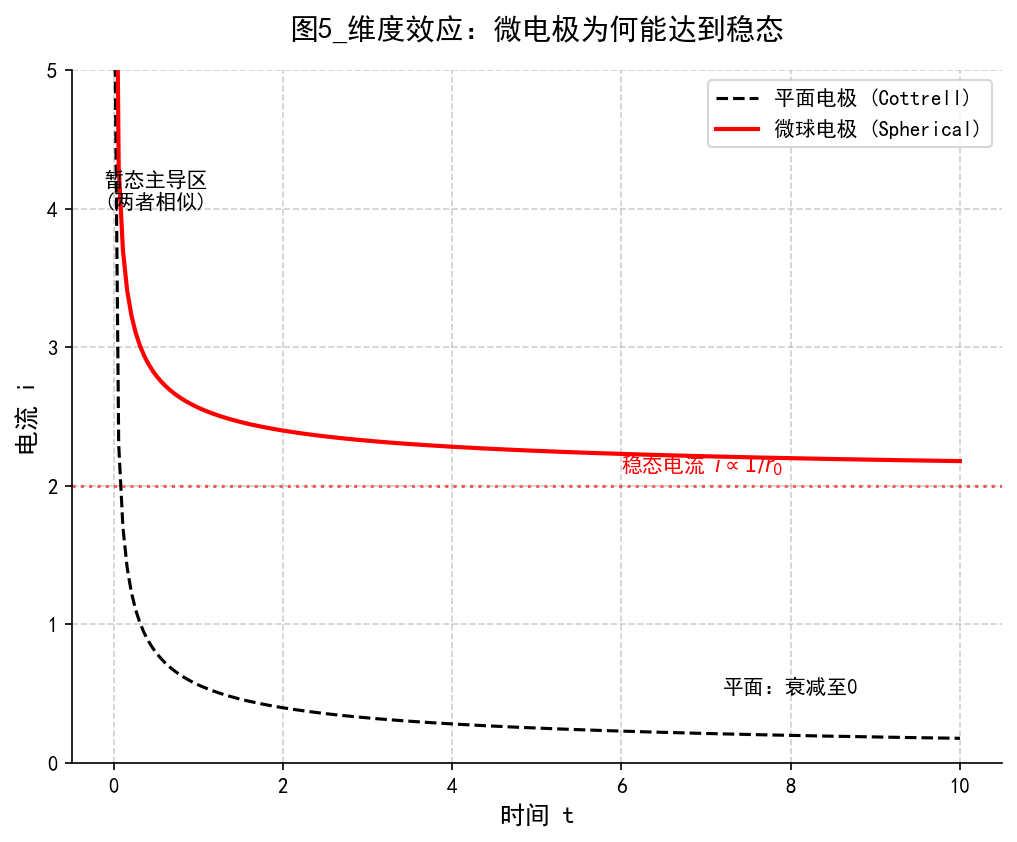
球形扩散:微电极的特殊性
在教材手写笔记(P160-162)中,专门讨论了球形扩散。这是理解微电极的关键。
维度带来的差异
平面电极是一维扩散,粒子只能垂直落下。球形电极是三维径向扩散,粒子可以从四面八方汇聚到一个点。
扩散方程的修正项
球坐标系下的菲克第二定律多了一项几何因子。求解后的电流公式包含两部分:
$$ i(t) = n F A D C^0 \left[ \frac{1}{\sqrt{\pi D t}} + \frac{1}{r_0} \right] $$
稳态与暂态的统一
这个公式完美展示了物理图像的演变:
- 短时间 ($t \to 0$):第一项(暂态项)占主导。因为扩散层很薄 ($\sqrt{Dt} \ll r_0$),球面看起来像平面,电流随时间衰减。
- 长时间 ($t \to \infty$):第一项趋于0,但第二项(稳态项)是常数!
$$ i_{steady} = \frac{n F A D C^0}{r_0} $$
微电极球形扩散
概念归纳
平面电极在静止溶液中永远达不到稳态(电流会一直衰减到0,因为 $\delta$ 无限增厚)。
但微球电极可以!因为对于微小的球体,扩散层向外扩张时,其体积迅速增大,从四面八方补给的物质足以维持一个恒定的梯度。这就是为什么微电极可以做稳态测量而不需要搅拌。
作者:GARFIELDTOM
邮箱:coolerxde@gt.ac.cn