核心概念归纳
核心在于研究电极过程的速率及其影响因素。这一理论体系的逻辑起点是电极的平衡状态,通过引入电流,观察其偏离平衡的现象(极化),然后探究现象背后的原因(基本历程和RDS),最终形成一套研究方法(极化曲线)。
电极的极化现象
1. 平衡态 (Equilibrium State)
- 定义: 处于热力学平衡状态的电极体系(可逆电极)。
特征:
- 氧化反应和还原反应速度相等(动态平衡)。
- 电荷交换和物质交换处于动态平衡。
- 净反应速度为零,外电路电流 $I=0$。
- 电极电位为平衡电位 ($\phi_{eq}$ 或 $\phi_{平}$)。
2. 极化现象的引入 (Introduction to Polarization)
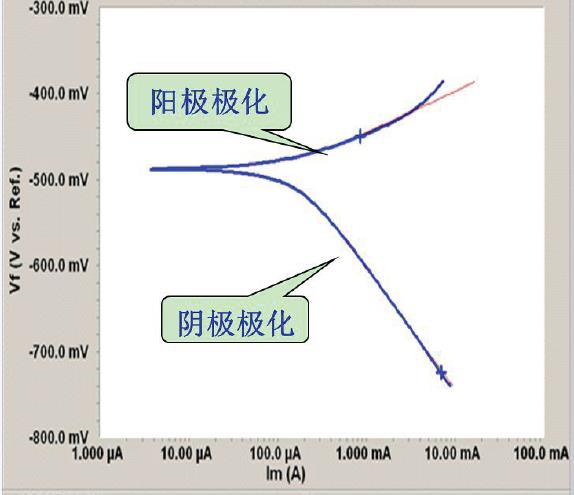
电极极化曲线示意图
- 极化定义: 当电极上有电流通过时,电极失去原有平衡状态,其电极电位偏离平衡电位的现象。
极化规律:
- 阴极极化 (Cathodic Polarization): 发生还原反应,电极电位 $\phi_c$ 偏离平衡电位 $\phi_{eq,c}$ 向更负方向移动 ($\phi_c < \phi_{eq,c}$)。
- 阳极极化 (Anodic Polarization): 发生氧化反应,电极电位 $\phi_a$ 偏离平衡电位 $\phi_{eq,a}$ 向更正方向移动 ($\phi_a > \phi_{eq,a}$)。
3. 极化程度的定量描述
过电位 (Overpotential, $\eta$) 是衡量极化程度的直接参数,是电极实际工作电位与平衡电位的差值。
$$\eta_c = \phi_{eq,c} - \phi_c$$
$$\eta_a = \phi_a - \phi_{eq,a}$$
注意: 教材中规定 $\eta$ 习惯取正值,故阳极极化时 $\eta_a = \phi_a - \phi_{eq,a}$,阴极极化时取 $\eta_c = \phi_{eq,c} - \phi_c$。
极化的实质与作用机制
1. 极化的实质 (Essence of Polarization)
电极极化的根本原因是:电子运动速度 ($v_{电子}$) 与电极反应速度 ($v_{反}$) 之间的矛盾。
- 逻辑递进: 电子在外电路中的传输速度极快,远大于电化学反应的化学变化速度($v_{电子} \gg v_{反}$)。当外加电流时,电极反应速度跟不上电子的供给或消耗速度,导致电荷在电极/溶液界面积累。
| 极化类型 | 电子与反应速度关系 | 净电荷积累 | 极化方向 |
|---|---|---|---|
| 阴极极化 | 电子流入电极速度 > 还原反应消耗电子速度 | 负电荷积累 | $\phi$ 向负移 |
| 阳极极化 | 氧化反应产生电子速度 > 电子流出电极速度 | 正电荷积累 | $\phi$ 向正移 |
2. 作用机制 (Polarization vs. Depolarization)
电极性质的变化取决于两种相互矛盾作用的对立统一:
- 极化作用 (Polarization Effect): 电子流动导致电极表面电荷积累,使电极电位偏离平衡状态。
- 去极化作用 (Depolarization Effect): 缓慢的电极反应吸收或释放电荷,使电极电位恢复平衡状态。
极化曲线
极化曲线是电化学动力学研究的基础工具。
1. 电极反应速度与电流密度的关系
在稳态条件下,电极反应的净速度 ($v$) 可以用外电路测得的净电流密度 ($j$) 来表示。
对于电极反应 $O + ne \rightleftharpoons R$:
非均相化学反应速度:
$$v = - \frac{1}{S} \frac{dc_O}{dt} = \frac{1}{S} \frac{dc_R}{dt}$$
法拉第定律关联:
$$j = nFv$$
结论: 当电极反应达到稳定状态时,实验测得的外电流密度 ($j$) 值就代表了电极反应的净速度 ($v$)。因此,极化曲线 ($\phi$ vs $j$ 或 $\eta$ vs $j$) 实际上反映了电极反应速度与电极电位之间的特征关系。
2. 极化曲线图像与概念关系
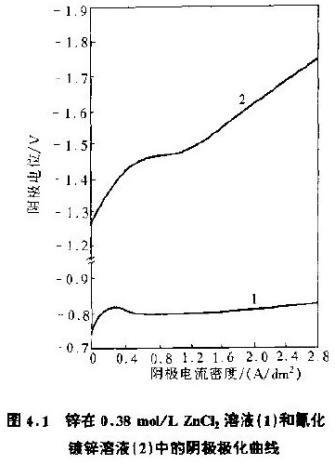
图2_锌在0.38mol/L $ ZnCl_2 $ 溶液(1)和氯化镀锌溶液(2)中的阴极极化曲线
- 图像关系: 极化曲线的形状(如斜率)直接反映了电极过程的动力学特性。
- 极化度 (Polarization Rate, $P$):
$$P = \frac{d\phi}{dj} \quad \text{或} \quad P = \frac{d\eta}{dj}$$
极化度在数值上具有电阻的量纲(反应电阻),斜率越大(即极化度越大),表明该电极过程进行越困难,受到的阻力越大。
电极过程的基本历程与速度控制步骤
电极过程不是一个简单反应,而是由一系列性质不同的单元步骤串联(有时并联)组成的复杂过程。
1. 电极过程的基本历程 (Basic Steps)
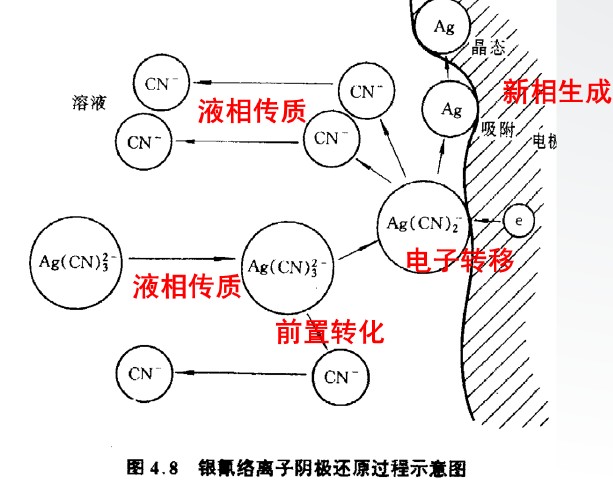
电极过程的基本历程示意图
| 序号 | 步骤名称 | 核心行为 | 动力学特点 | 极化类型 | 必需步骤 |
|---|---|---|---|---|---|
| (1) | 液相传质 | 反应粒子从溶液本体迁移到电极表面。 | 浓差极化 | 是 | |
| (2) | 前置转化 | 反应粒子在界面进行的电化学反应前的转化 (如吸附、脱溶剂化)。 | 无电子参与,速度与电极电位无关。 | 表面转化极化 | 否 |
| (3) | 电子转移 | 反应粒子在界面得失电子。 | 电化学极化 | 是 | |
| (4) | 随后转化 | 反应产物在界面进行的电化学反应后的转化 (如脱附、复合)。 | 表面转化极化 | 否 | |
| (5) | 新相生成 / 传质 | 产物离开界面或形成新相 (如晶体、气泡)。 | 浓差极化 / 电结晶极化 | 是 |
2. 速度控制步骤 (Rate-Determining Step, RDS)
- 化学动力学基础: 反应速度 ($v$) 与活化能 ($\Delta G^0$) 呈指数关系:
$$v \propto e^{-\Delta G^0 / RT}$$
不同步骤活化能不同,固有反应潜力不同。 - RDS 原理: 在串联过程中,各个单元步骤的实际净速度是相等的,并等于整个电极过程的净速度。
- RDS 定义: 各单元步骤中,速度最慢(即活化能最高)的电极过程决定了整个电极过程的速度,称为速度控制步骤。
- RDS 相对性: 各步骤的“快”与“慢”是相对的,当电极反应条件改变时(如强烈搅拌),RDS 可能会发生变化(如从传质步骤转变为电子转移步骤)。
3. 极化类型的分类 (Classification based on RDS)
电极极化根据谁是RDS进行分类:
| 极化类型 | 对应的RDS | 实质 |
|---|---|---|
| 浓差极化 (Concentration Polarization) | 液相传质步骤 (1 或 5) | 传质慢,导致电极表面反应粒子浓度低于溶液本体浓度,电位偏离。 |
| 电化学极化 (Electrochemical Polarization) | 电子转移步骤 (3) | 电子转移慢,导致电极表面得失电子的电化学反应迟缓,电位偏离。 |
| 表面转化极化 (Surface Conversion Polarization) | 前置或随后转化步骤 (2 或 4) | 界面化学转化慢,导致电位偏离。 |
准平衡态
1. 准平衡态的提出
- 理论依据: 控制步骤与非控制步骤的活化能差异巨大(可达几十个 kJ/mol),导致它们的速度相差千倍甚至万倍。
- 逻辑推导: 当电极反应以RDS的速度 ($j_{净}$) 进行时,非控制步骤 (快步骤) 的速度虽然也在变化,但它们原本的速度太快,相对于$j_{净}$来说,它们的净反应速度可以忽略不计。
以非控制步骤为例:
$$j_{净} = \vec{j} - \overleftarrow{j}$$
其中 $\vec{j}$ 为正向绝对速度,$\overleftarrow{j}$ 为逆向绝对速度。
因为非控制步骤的固有速度 $v_{固有}$ 远大于 $v_{净}$,即 $\vec{j}$ 和 $\overleftarrow{j}$ 远大于 $j_{净}$:
$$\vec{j} \gg j_{净}, \quad \overleftarrow{j} \gg j_{净}$$
因此,可以近似认为 $\vec{j} \approx \overleftarrow{j}$,非控制步骤的净反应速度为零。
2. 准平衡态的意义
非控制步骤虽然有电流通过,但其还原反应和氧化反应速度近似相等,仍接近于平衡状态。
- 简化问题: 处于准平衡态的步骤可以用热力学方法(如能斯特方程)来处理,无需使用复杂的动力学方法,从而简化了整个电极过程的分析。
原电池和电解池的极化
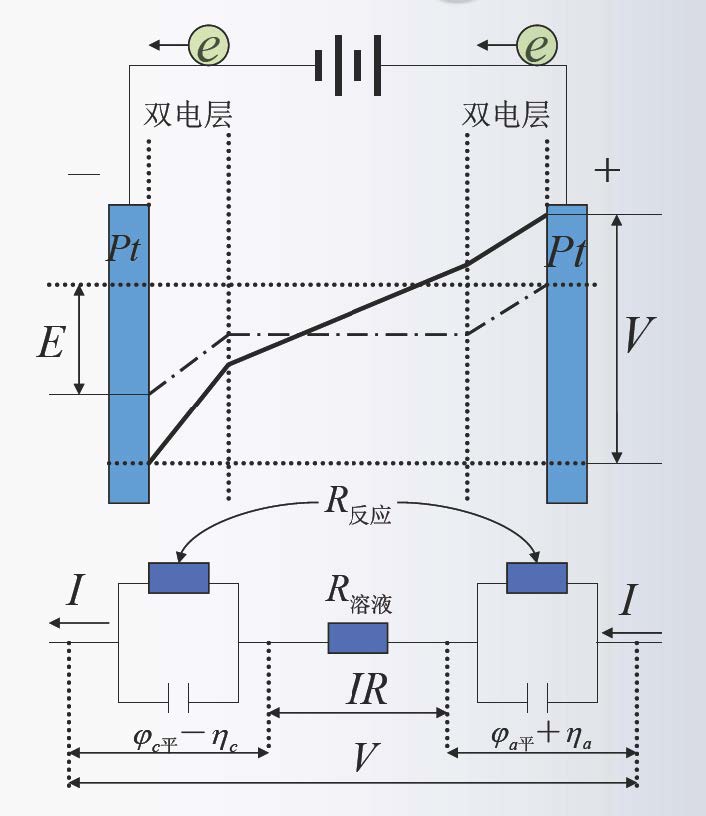
1. 电池超电压 ($V_{over}$)
电化学中,将两个电极的过电位之和 ($\eta_a + \eta_c$) 称为电池超电势(超电压) ($V_{超}$)。
$$V_{超} = \eta_a + \eta_c$$
2. 电池端电压的定量描述
欧姆降 ($IR$):溶液中由于电流通过产生的电阻降。其方向始终与电流方向相同。
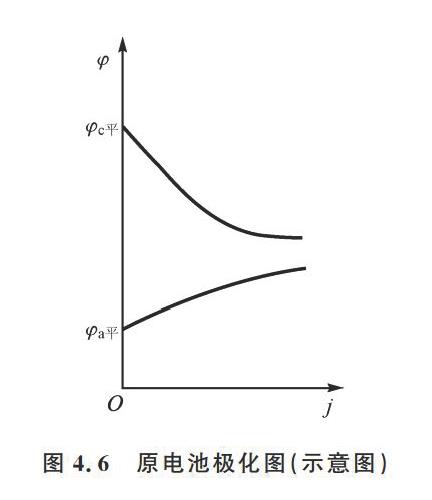
原电池 (Galvanic Cell, 自发过程):
原电池的极化规律示意图
- 电动势:$E = \phi_{eq,c} - \phi_{eq,a}$
- 端电压:
$$V = \phi_c - \phi_a - IR$$
$$V = (\phi_{eq,c} - \eta_c) - (\phi_{eq,a} + \eta_a) - IR$$
$$V = E - (\eta_c + \eta_a) - IR$$
$$V = E - V_{超} - IR$$
结论: 极化和欧姆降使原电池的端电压减小 ($V < E$)。
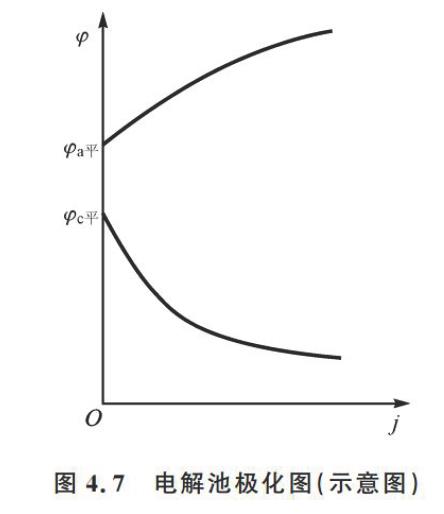
电解池 (Electrolytic Cell, 非自发过程):
电解池的极化规律示意图
- 理论电压:$E = \phi_{eq,a} - \phi_{eq,c}$
- 端电压:
$$V = \phi_a - \phi_c + IR$$
$$V = (\phi_{eq,a} + \eta_a) - (\phi_{eq,c} - \eta_c) + IR$$
$$V = E + (\eta_c + \eta_a) + IR$$
$$V = E + V_{超} + IR$$
结论: 极化和欧姆降使电解池的端电压增大 ($V > E$),所需电压升高。
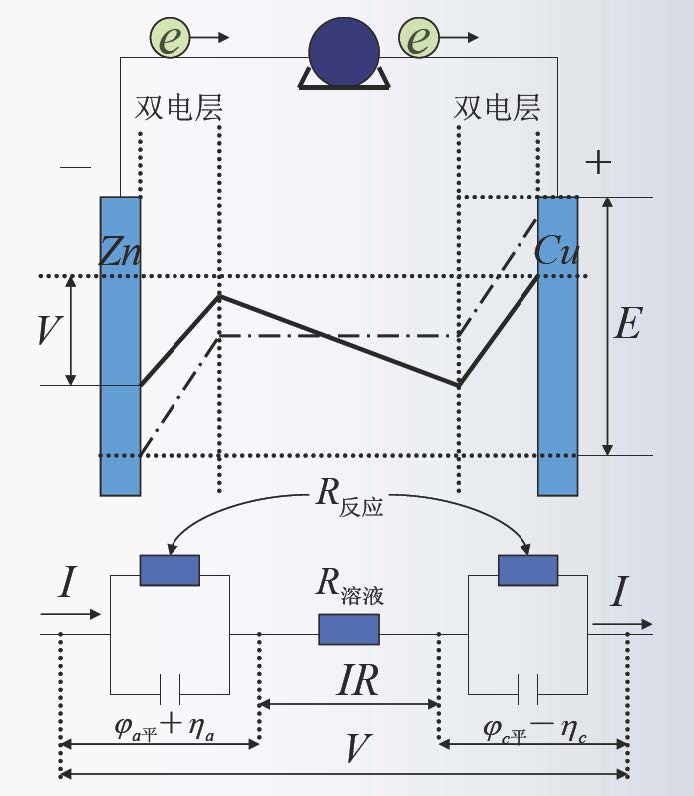
3. 极化图
为了更好的分析阴阳极的极化过程,我们将阴极极化曲线和阳极极化曲线,画在同一坐标系中组成的曲线图称为极化图。
原电池和电解池的 端电压 $ V $ 变化 主要来源于电极极化
电极过程的特征总结
电极过程是一种特殊的异相催化反应,具备以下特征:
- 异相催化动力学规律: 反应速率与界面性质(如表面积、活性中心、吸附)有关。
- 界面电场的重大影响与控制: 电极电位(界面电场)可人为、连续地改变,从而连续控制反应速率。这是电极过程区别于一般化学反应的最重要特征。
- 多步骤的复杂过程: 动力学规律由速度控制步骤 (RDS) 决定,非控制步骤处于准平衡态。
作者:GARFIELDTOM
邮箱:coolerxde@gt.ac.cn